Решить пример, все подробно и без логарифма
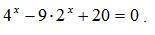
Другие вопросы по теме Алгебра
Популярные вопросы
- Найдите периметр треугольника если длины его сторон ровны 16см, 25см и 8...
2 - Реши упавнения y: 8=6,n*4=24,42: t=7...
1 - Всеобщая 9 класс! варшавский договор: 1)дата создания; 2)страны-участницы; 3)цели....
2 - Леший собрал для супа 12 грибов. но грибы оказались червивыми. сначала леший выбросил...
2 - Никита выписывает подряд целые числа 1,2, но он не любит цифру 7 и пропускает...
1 - Охарактеризуйте особенности иконописи галицко-волынского княжества...
2 - Звуко-буквенний аналіз слів незрівнянний, щедро...
3 - 5интересных вопросов на тему дворцолвые перевороты 7 класс...
3 - Ласточки заботливые родители . они вдвоем , чтобы выкормить птенцов делают за...
2 - Какое из утверждений верно? а)крупнейшими формами рельефа являются выступы материков...
1
Объяснение:
Введём замену:
Перепишем уравнение с учётом замены:
Решаем уравнение по теореме Виета:
Вернёмся к замене: