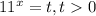решить показательные неравенства . 11^3x + 11^x+2 − 2 ∙ 11^2x = 0
(1/7)^(x+2)∙√7 = 7^(x−3)
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. What time do you get up? 2. Do you have a shower every day?...
2 - 1.Выбрать, что относится к средствам труда: а) машина;б) энергия,в)...
1 - Как накапливаются географические знания? - Как представляются результаты...
2 - Прочитайте Как вы думаете соответствует ли содержание текста тема...
3 - Вычислить определитель 2го порядка...
2 - Найдите грамматическую(-ие) ошибку(-и) в предложении(-ях). Запишите...
1 - 1) PH₃, HI, H₂O2) H2 Os, Naal...
2 - Написать анализ сцены убийства Оли Мещерской казачьим офицером....
2 - Уәзірлер не үшін шөптің жаманы деп шеңгелді алды? • 2. Уәзірлер...
2 - Вопросы и задания 1. Сравните государственное устройство кимаков...
1
либо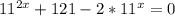
Замена