1. Алгебра
  2. Решить неравенство (x+7)(x^2-6x+8)^1/2

Решить неравенство (x+7)(x^2-6x+8)^1/2 >= (x+1)(x^2-3x+2)^1/2

Colka123 Colka123    2   29.07.2020 15:26    0

Ответы
насьть насьть  15.10.2020 15:34

(x+7)\cdot \sqrt{x^2-6x+8}\geq (x+1)\cdot \sqrt{x^2-3x+2}

ОДЗ:

\left \{ {{x^2-6x+8 \geq0 } \atop {x^2-3x+2\geq 0 }} \right.         \left \{ {{(x-2)(x-4) \geq0 } \atop {(x-1)(x-2)\geq 0 }} \right.     ⇒    x \in (-\infty; 1] \cup 2 \cup [4; +\infty)

Рассматриваем четыре  случая с учетом ОДЗ:

1) Если правая часть неотрицательна, левая  неположительна

\left \{ {{(x+1)\cdot \sqrt{x^2-3x+2}\leq 0} \atop {(x+7)\cdot \sqrt{x^2-6x+8}\geq 0}} \right.    ⇒  \left \{ {{x+1\leq 0 ; x=1; x=2} \atop {\left \[ {{x+7 \geq 0; x\leq 2 ; x \geq 4 }} \right. }} \right.     ⇒x \in [-7;- 1] U{1} U {2}

Неравенство верно при любых        x \in [-7;-1] U {1} U {2}

2)

Если правая часть отрицательная, левая неотрицательная, неравенство неверно:

   \left \{ {{(x+1)\cdot \sqrt{x^2-3x+2}\geq0} \atop {(x+7)\cdot \sqrt{x^2-6x+8}< 0}} \right.    ⇒  \left \{ {{x \geq-1} \atop {\left \[ {x     ⇒ нет таких  значений х

3)

Если правая часть неотрицательная , левая неотрицательная

\left \{ {{(x+1)\cdot \sqrt{x^2-3x+2}\geq0} \atop {(x+7)\cdot \sqrt{x^2-6x+8}\geq 0}} \right.⇒  \left \{ {{-1\leq x\leq 2; x \geq4} \atop {\left \[ {-7 \leqx\leq1; x \geq2}} \right.     ⇒ x \in [-1;1] \cup2\cup[4;+\infty)

 возводим обе части неравенства в квадрат:

(x+7)^2\cdot(x^2-6x+8)\geq (x+1)\cdot(x^2-3x+2)

(x+7)^2\cdot(x-2)\cdot (x-4)-( x+1)^2\cdot(x-1)\cdot (x-2)\geq 0

(x-2)\cdot((x-7)^2\cdot (x-4)-( x+1)^2\cdot (x-1))\geq 0

(x-2)\cdot(x^3+14x^2+49x-4x^2-56x-196-x^2+x-x^2+1)\geq 0

(x-2)\cdot(9x^2-6x-195)\geq 0

3\cdot (x-2)\cdot(3x^2-2x-65)\geq 0                      D=(-2)²-4·3·(-65)=784=28²

3\cdot (x-2)\cdot(3x+13)(x-5)\geq 0

x \in [-\frac{13}{3} ;2] \cup[5;+\infty)

C  учетом условия третьего случая:                     x \in [-1;1] \cup[4;+\infty)

получим ответ   третьего случая        x \in [-1;1] \cup [5;+\infty)

4)

Если левая  часть отрицательная и правая тоже отрицательна

\left \{ {{(x+1)\cdot \sqrt{x^2-3x+2}⇒  \left \{ {{x     ⇒ x \in (-\infty;-7)

умножаем на (-1) обе части неравенства и

 возводим  в квадрат:

(x+7)^2\cdot(x^2-6x+8)\leq (x+1)\cdot(x^2-3x+2)

(x+7)^2\cdot(x-2)\cdot (x-4)-( x+1)^2\cdot(x-1)\cdot (x-2)\leq 0

(x-2)\cdot((x-7)^2\cdot (x-4)-( x+1)^2\cdot (x-1))\leq 0

(x-2)\cdot(x^3+14x^2+49x-4x^2-56x-196-x^2+x-x^2+1)\leq 0

(x-2)\cdot(9x^2-6x-195)\leq 0

3\cdot (x-2)\cdot(3x^2-2x-65)\leq 0                      

D=(-2)²-4·3·(-65)=784=28²

3\cdot (x-2)\cdot(3x+13)(x-5)\leq 0

x \in (-\infty;-\frac{13}{3} ] \cup [2;5]

C  учетом условия четвертого  случая: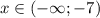                     x \in (-\infty;-7)

получим ответ   четвертого случая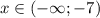        x \in (-\infty;-7)

Объединяем ответы рассмотренных случаев:

x \in (-\infty;1] \cup 2 \cup [5;+\infty)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
lerkakotik1983 lerkakotik1983  05.07.2019 03:50
Решите выражение -6(1/6-1/3y)-2(1-3 1/2y) если y= -2 3/5 30...
mariya8309662072 mariya8309662072  05.07.2019 03:50
Вдоме в котором живет женя один подъезд на каждом этаже по 12 квартир, женя живет в квартире 34.на каком этаже живет женя?...
БеднаяЕва БеднаяЕва  05.07.2019 03:50
Найти корень уравнения x/5 -2=x-86/25...
NEW4IK NEW4IK  26.08.2019 22:20
Решите уравнение: а)(х+2)(х^2-2х+4)-х(х+2)(х-2)=12...
JIuchno JIuchno  26.08.2019 22:20
Решите уравнение х(х+3)-4(х-5)=7(х+4)-8...
ilyavarbanetsozotem ilyavarbanetsozotem  20.05.2019 10:40
Перед входом в крепость сложена пирамида из одинаковых пушечных ядер (в треугольник, и ядра каждого следуещего слоя лежат в ямках предыдущего слоя). какаим может быть количество...
lavinaalina lavinaalina  20.05.2019 10:40
Найдитекоринки уравнения x в квадрате -1.3x=0 3x в квадрате -48=0...
TRЮM TRЮM  20.05.2019 10:40
Решите уравнение 9/x+5-4/x=0 решить, у меня с все хорошо, но почему-то не получается решить это уравнение. у меня получился х=4, мне кажется что я что-то сделала не так!...
Pomochnik1vsegda Pomochnik1vsegda  20.05.2019 10:40
Дана арифметическая прогрессия: ; -70 ; -53 ; - первый положительный член этой...
morti3 morti3  20.05.2019 10:40
Тело движется прямолинейно в вертикальном направлении по закону h(t)=2+9t-4t2 (t - время движения в секундах, h - расстояние в метрах от земли до тела). определите скорость...

Популярные вопросы