решить неравенство методом интервалов
Другие вопросы по теме Алгебра
Популярные вопросы
- Назвіть речові та пмсьменні історичні джерела які можна використовувати для...
1 - Найдите сторону равностороннего треугольника, если радиус описанной около него...
1 - Решить[tex] \sqrt{2} \sin( \frac{x}{2} ) - \sqrt{2} \cos \frac{x {}^{2} }{2}...
1 - Что больше сила архимеда или сила тяжести...
1 - Кате 12 лет что составляет одна третья возраста ее матери а возраст матери...
1 - Впрямоугольном треугольнике авс угол с равен 90° а угол а равен 45 ° сравните...
3 - Если a * b 0, то угол a между ними (вектор)...
1 - Как можно предотвратить заражение простейшими, которые вызывают кишечные заболевания...
1 - Сочинение из этих слов : sportsman , run , olympic flame , yellow , greece...
3 - Два прямоугольниа заданы длинами сторон.определить,можно ли 1 прямоугольник...
1
ответ :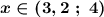
Объяснение:
ОДЗ :
Возведем в квадрат
Данный промежуток удовлетворяет ОДЗ :
ответ :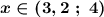
В левой части стоит квадратный корень, который неотрицателен . Значит он может быть меньше только положительного выражения . Но сумма квадр. корней тоже неотрицательна . Поэтому условие положительности суммы квадр. корней можно не писать .
ОДЗ: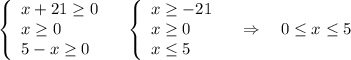
Возведём в квадрат обе части неравенства .
Теперь неравенство будет эквивалентно совокупности двух систем.
Нашли нули функции .
.
Решаем неравенство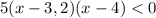 методом интервалов. Наносим нули функции на числовую ось и вычисляем знаки на получившихся промежутках . Надо выбрать любое число, принадлежащее интервалу , подставить его в функцию, и определить , какой знак принимает ф-ция в нужном интервале .
методом интервалов. Наносим нули функции на числовую ось и вычисляем знаки на получившихся промежутках . Надо выбрать любое число, принадлежащее интервалу , подставить его в функцию, и определить , какой знак принимает ф-ция в нужном интервале .
Например,