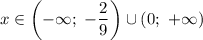Решить неравенство:
f ' (x) > 0, если f(x) = 9х3 + 3х2
Другие вопросы по теме Алгебра
Популярные вопросы
- Реши задачу, пошагово выполняя указанные действия и заполняя пропуски....
2 - What do you see on the picture? 2. How do you call the large red object?...
2 - Найди значение выражения 2х(m³+15),если m=3...
2 - Закончить уравнения реакций, назвать продукты: 1) Н,+ СІ, переход электронов2)...
1 - Решить неравенство, с объявлением: ...
2 - Побудувати графік квадратичної функції за схемою будови y=2x^2-9x+4...
1 - Составьте краткий конспект по теме Особенности природы Африки....
2 - Представь информацию в виде схемы о организации чем занимаются руководители...
1 - у меня экзамен ! 2 .Определить валентность в формулах Pb(NO3)2 N2O5 Ca3P2...
2 - 1) Перескажи, как звери проводили лето. 2) Как ты понял значение слова...
3
Решим неравенство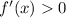 , то есть
, то есть 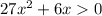
ответ: