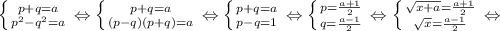решить неравенство
а - параметр
Другие вопросы по теме Алгебра
Популярные вопросы
- Во сколько раз гидростатическое давление в охотском море в воде на глубине...
1 - На соревнованиях по кольцевой трассе первый велосипедист проходил круг...
1 - На сколько процентов изменится площадь прямоугольника, если длину каждой...
2 - Докажите тождество: (1/x+2/y+x/y^2) : y^2-x^2/xy+2/x-y=-1/y надл ! !...
1 - Упав на землю вертикально, мяч отскочил на 3,2 м. модуль скорости, с которой...
1 - (2х-1)²-25 . разложите на множители...
3 - Серединные перпендикуляры к сторонам abи cdчетырехугольника abcd пересекаются...
1 - Ph-это бензольное кольцо! расположите следующие соединения в порядке увеличения...
1 - Могут ли две молекулы бутадиена-1,3 вступать в реакцию дильса-альдера?...
1 - Как найти cosx, tgx, ctgx если sinx=1/5. 0...
3
Перенесём корень из икс направо и возведём в квадрат обе части.
a + x < a² - 2a√x + x, сократим на х и преобразуем: 2a√x < a² - а.
Сократим на а: 2√x < a – 1.
Отсюда находим, что а > 1 (левая часть не может быть отрицательной), а также, что х > 0.
Возведём в квадрат обе части.
4x < a ²– 2a + 1.
ответ: а > 1,
x < (1/4)*( a ²– 2a + 1).
a≤1⇒решений нет; a> 1⇒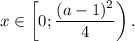
Объяснение:
Левая часть неравенства неотрицательна, поэтому при a≤0 решений нет.
Пусть a>0. Рассмотрим функцию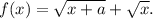 Это возрастающая функция на своей области определения
Это возрастающая функция на своей области определения 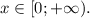
Если![a\in(0;1],](/tpl/images/4978/0954/d6235.png)
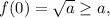 а тогда в силу возрастания f(x)≥a на области определения, поэтому при таких a решений нет.
а тогда в силу возрастания f(x)≥a на области определения, поэтому при таких a решений нет.
Пусть a>1. В этом случае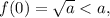 и нам нужно поймать момент, когда f(x) станет равен a. Итак, решаем уравнение
и нам нужно поймать момент, когда f(x) станет равен a. Итак, решаем уравнение 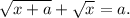
Обозначим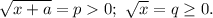 Поскольку p²-q²=a, уравнение равносильно системе
Поскольку p²-q²=a, уравнение равносильно системе