Решить неравенство:
1.|(корень 2х) + 1 | <=1
2.| 1 - 2x| > 1/3

Question

Алгебра: Решить неравенство: 1.|(корень 2х) + 1 | =1 2.| 1 - 2x| 1/3

ЛизаБугакова · Answer

1. ОДЗ: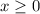  С учетом ОДЗ, где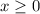   , получаем решение: ответ: {0}2.Раскрываем модуль и получаем два неравенства:1)  Решаем первое                                  2)   Решаем второе                                   3)    Общее решение: (-∞;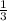  ) + (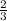;  +∞)   ответ: (-∞;  ) ∪ (;  +∞)...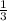

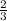Решить неравенство: 1.|(корень 2х) + 1 | <=1 2.| 1 - 2x| > 1/3

Популярные вопросы

Решить неравенство:
1.|(корень 2х) + 1 | <=1
2.| 1 - 2x| > 1/3