Решить не через дискриминант
, !

ответ: 1.5 часа.

Объяснение:

учить все квадраты совсем нет необходимости... в редкой задаче встречаются квадраты чисел, больших 25

достаточно грамотно пользоваться формулами сокращенного умножения и приемами разложения на множители при вычислении дискриминанта и корни будут "извлекаться сами"...

ведь если уравнение квадратное,

то для решения или т.Виета (устно) или дискриминант))

за t обозначим время, которое нужно найти;

тогда путь S₂ = 27 км, время t,

скорость на этом участке пути v₂ = S₂/t = 27/t

путь S₁ = 67-27 = 40 км, время 4-t,

скорость на этом участке пути v₁ = S₁/t = 40/(4-t)

получили уравнение: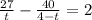

2t*(4-t) = 108-67t

2t² - 75t + 108 = 0

D = 75*75-4*2*108 = 9*25*25-8*4*27=9*(625-96)=(3*23)²

t₁ = (75+69)/4 = 144/4 > 4 часов--посторонний корень

t₂ = (75-69)/4 = 6/4 = 3/2 = 1.5

1,5 часа

Объяснение:

Пусть велосипедист проехал 27 км со скоростью х км/час, тогда

67-27=40 км он проехал со скоростью х-2 км/час. Составим уравнение:

27/х + 40/(х-2) = 4

27х-54+40х-4х²+8х=0

4х²-75х+54=0

х=(75±√(5625-864))/8=(75±√4761)/8=(75±69)/8

х₁=3/4 (не подходит) и х₂=18.

Скорость велосипедиста на участке 27 км была 18 км/час.

27:18=1,5 часа он затратил на этом участке.