1. Алгебра
  2. решить найти кол во корней

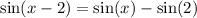
решить \sin(x - 2) = \sin(x) - \sin(2)
найти кол во корней на промежутке
[0;2п]

Аннаlove2017 Аннаlove2017    3   01.01.2022 00:17    0

Ответы
polo73oye61z polo73oye61z  01.01.2022 01:00

(см. объяснение)

Объяснение:

\sin(x-2)=\sin x-\sin2\\\sin\left(2\cdot\dfrac{x-2}{2}\right)=2\sin\dfrac{x-2}{2}\cos\dfrac{x+2}{2}\\\sin\dfrac{x-2}{2}\cos\dfrac{x-2}{2}=\sin\dfrac{x-2}{2}\cos\dfrac{x+2}{2}\\\sin\dfrac{x-2}{2}\left(\cos\dfrac{x-2}{2}-\cos\dfrac{x+2}{2}\right)=0\\\sin\dfrac{x-2}{2}\sin\dfrac{x}{2}=0

Произведение равно 0, когда хотя бы 1 из его множителей равен 0, а другие при этом не теряют смысла.

Тогда:

\left[\begin{array}{c}\sin\dfrac{x-2}{2}=0sin\dfrac{x}{2}=0\end{array}\right;

Для первой строки совокупности:

\sin\dfrac{x-2}{2}=0\\\dfrac{x-2}{2}=n\pi,\;n\in\mathbb{Z}\\x=2+2n\pi,\;n\in\mathbb{Z}

Для второй строки совокупности:

\sin\dfrac{x}{2}=0x=2k\pi,\;k\in\mathbb{Z}

Итого получили, что ответ:

\left[\begin{array}{c}x=2+2n\pi,\;n\in\mathbb{Z}\\x=2k\pi,\;k\in \mathbb{Z}\end{array}\right;

Найдем теперь количество корней уравнения на промежутке [0;\;2\pi].

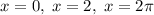Это: x=0,\;x=2,\;x=2\pi.

Тогда ответом будет число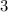 3.

Задание выполнено!

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ЛалKа228 ЛалKа228  04.05.2021 21:25
очень нужно. Если можно, то с объяснением на листке. Заранее благодарю​...
Gazizianov2018 Gazizianov2018  04.05.2021 21:24
Дослідити функцію y = 3x4 – 4x3 + 1 і побудувати її графік....
тяпница13 тяпница13  04.05.2021 21:21
1. Составьте приведенное квадратное уравнение, сума корней которого равна 6, а произведение- числу 4 2.Найдите стороны прямоугольника, если одна из них на 3 см меньше другой,...
egorcop egorcop  04.05.2021 21:19
очень нужно. Если можно, то с объяснением на листке. Заранее благодарю​...
SaminaR SaminaR  10.06.2019 21:50
1) cos8,5п 2) sin(-3,5п) , заранее : (...
Anna9411 Anna9411  10.06.2019 21:50
Контрольное ! : ** в магазине продано 200 кгземлянике, что составило 4/5 всей в магазин землянике. сколько кг землянике в магазин?...
54876 54876  10.06.2019 21:50
Решить систему уравнений а) методом подстановки х+2у=4 3х-4у=2 б) методом сложения 5х-6у=7 10+6у=8 в) графическим у-х=5 2х+у=-3 неужели никто не...
Racamaxa Racamaxa  10.06.2019 21:50
Представьте дробь 5n²+3n+6 \ n в виде суммы двучлена и дроби.выясните , при каких натуральных n данная дробь принимает натуральные значения. (\-дробная черта) за...
Димооон04 Димооон04  10.06.2019 21:50
Запишите четыре первых члена арифметической прогрессии, если а1 = 2, d= -3. решить : (...
Xadice12345 Xadice12345  10.06.2019 21:50
Какая функция называется ограниченной? а какая чётной?...

Популярные вопросы