Решить наибольшее значение функции f(x)=1+8x-x² на [2; 5] наименьшее f(x)=3x²-12x+1 на [1; 4]
Ответы
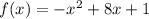
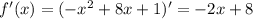
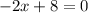
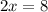
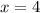
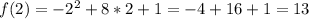
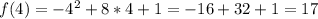 - наибольшее
- наибольшее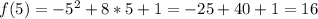
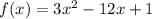
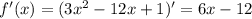
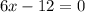
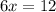
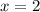
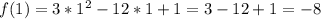
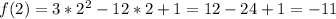 - наименьшее
- наименьшее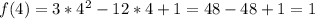
Другие вопросы по теме Алгебра
Популярные вопросы
- При каком значении x: а) значение выражения 5x равно -1 б) значение выражения...
1 - С! оптическая сила линзы равна 5 диоптрий. чему равно фокусное расстояние...
1 - Предложения составить со словами тоже и то же; также и так же.. ....
2 - Мини-рассказ на тему охрана воздуха от загрязнений...
3 - Две бригады состоящие из рабочих одинаковой квалификации одновременно начали...
1 - Для того, чтобы обеспечить одного человека чистым воздухом,необходимо растения...
3 - 1любое натуральное число является элементом множества целых чисел 2 любое...
3 - Тело массой 5 кг движется вертикально вверх с ускорением 2м/с^2.определите...
1 - Вкаком времени стоит предложение: it began to rain....
3 - Осень в лесу красива.-найти подлежащее и сказуемое...
2