решить метолом интервалов:
sqrt(x+8)>=x+2
Другие вопросы по теме Алгебра
Популярные вопросы
- Питання по роману айвенго (1-8 розіли)...
1 - Можно ли назвать городничего из произведения ревизор человеком.почему...
2 - Составьте план сочинения сочинение «моя комната» . у меня есть...
1 - Как расчитать площадь прямоугольника?...
3 - Укімнаті завдовжки 8 м ширина становить 75 % довжини а висота...
2 - ответьте на вопросы, биология 6 класс: 1.назовите самый крупный...
3 - Сместоимениями! 1. i don’t know these boys. do you know a) him...
1 - Люди добрые написать эссе про робинзона круза на казахском языке...
1 - Периметр прямоугольника 32см одна сторона прямоугольника 6см.сколькими...
3 - 20 найдите значение выражения: (-1/12+2/,36-0,64)-1-целая 13/15...
2
Объяснение:
ОДЗ: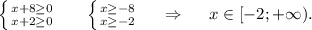
-∞__+__-4__-__1__+__+∞ ⇒ x∈[-4;1].
ответ: x∈[-2;1].