∫![\frac{dx}{\sqrt[3]{8x} }](/tpl/images/4018/7823/d8e61.png) решить
решить
максимально подробно потому,что хочу понять как решать.
Заранее благодарю!
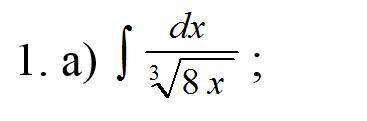
Другие вопросы по теме Алгебра
Популярные вопросы
- Фізика. Геометрична оптика. Закон прямолінійного поширення світла. Задача: Людина...
1 - 1.Прочитать стр.73-74 (Иссыкский курган) + конспект урока 2. Сделать краткую...
1 - БЛ нужно Димаш Құдайберген – халықаралық дәрежедегі танымал әнші Мәтін оқырманды...
1 - Вывести произвольную последовательность символов и определить, есть ли среди...
2 - В електронній касі у двох комірках містяться кошти в розмірі a грн та bгрн....
3 - Назови произведения в котором, мрачьна и окружающая героя природа...
2 - Трое маляров работали с одинаковой производительностью труда и получили за выполненую...
2 - Имеем выражение ( * )^4 = c^20. Что должно стоять вместо звёздочки?...
2 - очень! Нужно написать историю: We want stories for our magazine. Your story...
2 - 2-тапшырма өзүңүз каалагандай кыла бериңиз, мисалы менин атым Дайыр, анан мен...
2
Интеграл табличный..
Объяснение: