решить логарифмическое уравнение с подробными объяснениями
P.S если понадобится ответ, чтобы свериться, можно написать в коммы, и я отвечу
Другие вопросы по теме Алгебра
Популярные вопросы
- У помідорів нормальна висота і червоний колір плодів – домінантні ознаки,...
3 - с контрольной по географии...
2 - Комедия ,,горе от ума сравнение Чацкого и Молчалина (кратко)...
2 - ПОМАГИТЕЕЕ НАЙДИТЕ 10 СЛОВ СВЯЗАННЫХ С СУПЕРМАРКЕТОМ...
1 - Автолюбитель повертався додому з полювання на власній автомашині з причепом....
2 - как хорошо, что в нашем классе учатся ребята разных национальностей сочинение....
1 - Порівняйте зміст ст. 3 і 6 Декларації зі змістом ст. 5 Конституції України:...
2 - Найди некоторые решения каждого неравенства.45-х 19h*2 12d:3 7...
2 - Площадь квадрата равна 64 найдите радиус вписанной в квадрат окружности ...
1 - Издержки производства 60 шт. некоторого товара составляют 250 руб., а 90 шт....
2
Рассмотрим два случая: x > -3 и x < -3
Сначала первый:
Из условия раскрытия модуля если среди этих чисел есть корень, то это только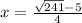 , но его нужно проверить по ОДЗ.
, но его нужно проверить по ОДЗ.
Теперь рассмотрим уравнение при x < -3
Учитывая раскрытие модуля, выбираем только один из корней, а именно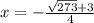
Теперь рассмотрим ОДЗ:
Cравним первый корень с 3, а второй с -5
Вроде оба корня подходят.