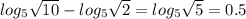Решить логарифмические уравнения 1 log2(x^2-2x)=3 2 2log3(-x)=1+log3(x+6) 3 log {3} 27-log{1/7} 7 4 2 в степени 1+log{2}5 5 lg4+2lg5 6 log{5}корень из 10 - log{5}корень из 2
Другие вопросы по теме Алгебра
Популярные вопросы
- Муравьишка добирался до своего муравейника. Сначала он ехал 9 мин...
1 - Скажите как это решить чтобы в Х поставить число...
2 - решить или же дайте ссылку где можно списать...
3 - , скиньте ответы на этот учебник (Л. И. Мальцева русский язык, подготовка...
3 - Условие задания: Марина Павловна внимательно изучает цены в каталогах,...
2 - В треугольнике СDE с углом E, равным 32 градуса, проведена биссектриса...
3 - Критичний аналіз існуючих класифікацій природних ресурсів1. Складіть...
1 - У чому полягає актуальність твору Усмішка бредбері...
3 - Два мотоциклиста стартуют одновременно в одном направлении...
1 - Что означает слово церковь...
2
1)ОДЗ: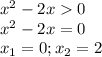
\\\+\\\(0)...-...(2)\\\+\\\=>
2)ОДЗ: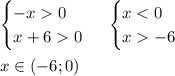
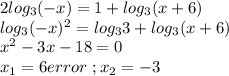
3)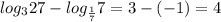
4)
5)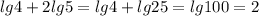
6)