решить линейные неравенствв
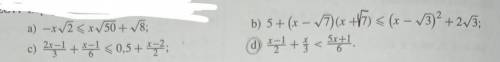
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему у мальчик нет имени? (рассказ: мальчик с коньками)...
2 - Бесит ! ☻☻☻ нужно написать про канаду по плану который внизу ↓↓↓ 1)положение...
1 - Обьём прямоугольного параллепипеда 302,4в кубе,а площадь его основания...
3 - 1)в треугольнике угол m=44°, а угол n меньше угла k в 7 раз. найдите...
3 - 2460: b=1332-1250 реши уравнение y-476-1056=154...
3 - Почему , на ваш взгляд, возникают чаще всего в зонах, прилегающилх к...
1 - Образуйте от данных существительных форму множественного числа. поставьте...
2 - Трьома машинами 350ц піску.скільки центнерів піску перевезли кожною...
1 - Запиши в таблицу годы великих сражений в 10-15 веках...
2 - Напишите сочинение-доказательство на тему книги-мои друзья по плану...
1
Объяснение:
а) х(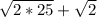 ) ≥ -
) ≥ -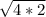
х5√2≥ - 2√2
5х ≥ -2
х ≥ -2/5 х ∈[-2/5; +∞)
b) 5+ x² - 7 ≤ x²-2√3 + 3 - 2√3
x²-2≤x²+3
при любом x, x ∈ (-∞; +∞)
с) умножим обе части почленно на 6
4х-2+х-1 ≤3+3х-6
5х-3 ≤3х-3
2х ≤0
х≤0 x∈(-∞;0]
d) умножим обе части почленно на 6
3x -3 + 2x < 5x+1
5x-3< 5x+1
при любом x, x ∈ (-∞; +∞)