1. Алгебра
  2. Решить lim х стремяшиеся

Решить lim х стремяшиеся к бесконечности (1+1/3х)^х

natalyabuben0111 natalyabuben0111    2   12.03.2019 17:30    1

Ответы
asdasdgasf asdasdgasf  25.05.2020 01:39

\lim_{x \to \infty} (1+\frac{1}{3x})^x=\{\frac{1}{3x}=\frac{1}{a}, a=3x, x=\frac{1}{3}a, x \to \infty, a \to \infty \} = \\ \lim_{x \to \infty} (1+\frac{1}{a})^{\frac{1}{3}a}=\lim_{x \to \infty} ((1+\frac{1}{a})^a)^{\frac{1}{3}}= \\ (\lim_{x \to \infty} (1+\frac{1}{a})^a)^{\frac{1}{3}}=e^{\frac{1}{3}}

ПОКАЗАТЬ ОТВЕТЫ
rus200130 rus200130  25.05.2020 01:39

Это второй замечательный предел:

Нужно только сделать некоторые преобразования:

Сделаем замену t=3x

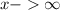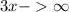
Поскольку x-\infty то и 3x -\infty

Перепишем наш предел с учетом этой замены:

\lim_{t \to \infty} (1+\frac{1}{t})^{\frac{t}{3}}= \\ =\lim_{t \to \infty} ((1+\frac{1}{t})^{t})^{\frac{1}{3}} 

Поскольку известно что:

\lim_{t \to \infty} (1+\frac{1}{t})^{t}=e 

то

 \lim_{t \to \infty} ((1+\frac{1}{t})^{t})^{\frac{1}{3}}=e^{\frac{1}{3}}=\sqrt[3]{e}

 

 ответ: \lim_{x \to \infty} (1+\frac{1}{3x})^x=\sqrt[3]{e}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
tropinaksusha tropinaksusha  10.04.2020 16:53
Найти сумму биномиальных коэффициентов седьмой строки...
kondratenkoari1 kondratenkoari1  10.04.2020 16:53
решить Преобразование тригонометрических выражений...
evelina2023 evelina2023  10.04.2020 16:53
Найдите сумму и произведение корней уравнения + 7х + 1 = 0 1) 1 2) -1 3) 7 4) -7...
милота0011 милота0011  10.04.2020 16:53
Выбери дроби, равные данной z−8/z2−11...
marusy552 marusy552  10.04.2020 16:52
Сколько трёхзначных чисел можно составить из цифр 0, 1, 6, 7, 8 при условии, что цифры в числе не повторяются?...
jenkatimosh jenkatimosh  10.04.2020 16:52
Разность арифметической прогрессии 1 член которой равен 8,5 а сумма 16/1 членов составляет 172...
AnnHaylen AnnHaylen  10.04.2020 16:52
1. Составить треугольник Паскаля до 8 степени....
lilipute2017 lilipute2017  10.04.2020 16:52
Найди , если 2^2t=16. (2t-степень решите))...
даня1163 даня1163  26.05.2019 22:00
Одно число больше другого на 6.а относятся они,как 9: 7.найдите эти числа....
KirillK2014 KirillK2014  26.05.2019 22:00
1. в каких координатных четвертях расположены точки: а( 25; 362); в( -3; 3\7); с( 0,25; -1,75); d(-0,001; -101,1)?...

Популярные вопросы