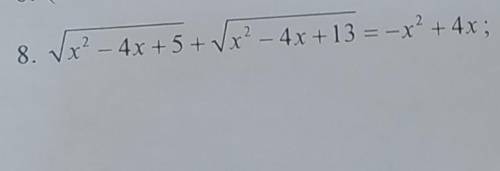
Алгебра: решить иррациональное уравнение

решить иррациональное уравнение

Ответы

оьмдды 13.01.2022 22:00

Объяснение:

$\sqrt{x^2-4x+5} +\sqrt{x^2-4x+13} =-x^2+4x$

сделаем оценку левой и правой частей

$\sqrt{x^2-4x+5} +\sqrt{x^2-4x+13} =\sqrt{x^2-4x+4+1} +\sqrt{x^2-4x+4+9} ==\sqrt{(x-2)^2+1} +\sqrt{(x-2)^2+9} \geq \sqrt{1} +\sqrt{9}=1+3=4$

а справа у нас парабола, ветви вниз, наибольшее значение

она принимает в вершине

$x_0=\dfrac{-b}{2a} =\dfrac{-4}{-2}=2y_0=-4+4\cdot2= 4$

левая часть уравнения ≥ 4, а правая ≤ 4

решение есть, если левая и правая части = 4

$-x^2+4x=4\\x^2-4x+4=0\\(x-2)^2=0boldsymbol{Otvet: x=2}$

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

yadianamelnik 27.07.2019 09:30

Найдите значение выражения ответ: 0.25 ·...

sapro95 27.07.2019 09:30

Nastyusha222 27.07.2019 09:30

Построить график функции y=|2x-1|-3x...

диана2440 25.11.2020 13:39

maksategemberdi 25.11.2020 13:39

7(x-1) 6x -4(3x+1) до ть...

ylianа06 25.11.2020 13:40

Портнягин 25.11.2020 13:40

7а-2b-5а+6b приведите подобные слагаемые памагит...

enc0r3 25.11.2020 13:40

AzNas 25.11.2020 13:40

pinok21rus 21.07.2019 06:10