решить эти задания, желательно с объяснением заранее
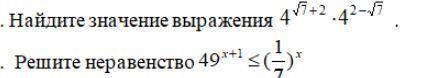
Другие вопросы по теме Алгебра
Популярные вопросы
- Захват монголами Владимира что на этой картинке характерно только для монгольской...
2 - 1.Зима, затруднявшая военные распоряжения, проходила, и наши генералы готовились...
1 - Какими химическими свойствами обладает оксид Сa. Напишите соответствующие уравнения...
2 - Постройте угол: 1) косинус которого равен 1/4; 2) котангенс которого равен 1/2;...
3 - Стороны оснований правильной усеченной четырехугольной пирамиды равны 8 см и 6...
1 - Опишите личность Леонардо да Винчи в качестве художника изобретателя учёного писателя...
3 - Попс формула Моцарт сальери...
1 - На уроке математики мы (что делаем?) и...
1 - Тема: кризові римські явища в Римській імперії. во наскільки раби були зацікавлені...
2 - В 300 граммах воды растворили в 125 г раствора сульфата меди (2). Определите массовую...
2
Отметьте лучшим решением и поставьте сердечко
Начнем с первого пункта.
Так как основания одинаковы (равны 4), мы можем упростить по формуле:
Подставляем.
Пункт второй.
В данном случае нужно самому привести к общему основанию.
49 - это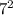 , а
, а  - это
- это  .
.
Значит,
А вот тут, так как это неравенство, где основания уже одинаковы, т.е. равны 7, мы можем убрать основания, оставив только степени. Опять же, это можно делать только если основания одинаковы.