Решить дробно-рациональное уравнение: 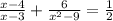
Очень Нужно!
Другие вопросы по теме Алгебра
Популярные вопросы
- Ятворительный падеж, исполнен всяческих надежд. творите! -чем? творите! - с кем?...
1 - Dvd-плеер elenberg не раскручивает диск. пробовал и с dvd и с cd дисками,так...
1 - Что такое мануфактуры? какие мануфактуры вы знаете?...
3 - Масса покоя поезда 2000 т .на сколько увеличивается его масса во время движения...
3 - Начерти прямоугольник длина которого 7 см. что на 5см больше ширины. найди периметр...
3 - H2so4 (серная кислота) является оксидом?...
2 - 1.какое количество вещества хлора и калия образуется при разложении 3 моль хлорида...
2 - Чем вас заинтересовала книга хоббит или туда и обратно?...
2 - Зубатый кит имеет 260 зубов, а амазонский дельфин - 140. сколько нужно взять...
3 - Синтаксический работ предложения- её верхушка высоко поднялась над другими деревьями....
3
Объяснение:
ОДЗ:
Решим уравнение по теореме Виета:
Корень х₂ не удовлетворяет ОДЗ.
решение на фотографии