Решить дифференциальные уравнения
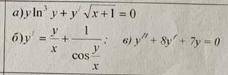
Другие вопросы по теме Алгебра
Популярные вопросы
- Какие предметы хранятся в музее истории космодрома? (приведи 2-3 примера)...
3 - Морфологический разбор слова по составу отдыхая .И нужно что бы присутствовали...
3 - Выберите немецкие глаголы, соответствующие указанной категории. 1 Переходный...
1 - Як властивості води пов язані зі структурою її молекули? ...
1 - Скласти розгорнутий план на тему розвиток культури україни за більшовицького...
2 - Уақытты тиімді пайдалану үшін не істеу керек? Тыңдарманныңназарын аудару...
3 - Преоброзуй неправильные дроби в смешанные числа...
2 - Кому поклонялись арийские племена? нужно...
2 - Бжб казак тили 5 ссынып с третьей задачай...
3 - 2sinx-√3=(0;6)cos5x+cosx=0...
2
a)
Это ДУ с разделяющимися переменными.
общее решение
2.
однородное ДУ
общее решение
3.
Однородное линейное ДУ
общее решение