решить дифференциальное уравнение и выполнить проверку
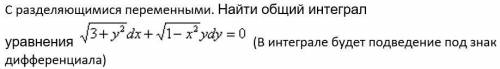
Другие вопросы по теме Алгебра
Популярные вопросы
- Дайте определение понятиям: строительная индустрия и промышленность...
2 - Осуществить преобразования 1) cu cuo cuso₄ cu(oh)₂ cuo 2) fe fe₂o₃...
1 - нужно ! найдите целое значение а, при котором уравнение 3x^2+а^2x+12a+4=0...
3 - Розвяжи рівняння 1. x×100-94=406 2. x×90+30=300...
2 - Сколько молекул находится в 1,5 моль hci? ответ запишите числом...
3 - 1. движение декабристов. “северное” и “южное” общества. предпосылки...
1 - Уравнение с двумя переменными, где одна уже известна. дано уравнение:...
2 - Часть 1-го сорта в некоторой продукции в среднем составляет 80%....
2 - У=in(x-10)×arccos^2×4x производная! !...
2 - Языки программирования высокого уровня являются...
3
Проверка: