Решить! число 5 представьте в виде суммы двух положительных слагаемых так , чтобы произведение первого слагаемого

Question

Алгебра: Решить! число 5 представьте в виде суммы двух положительных слагаемых так , чтобы произведение первого слагаемого и второго, возведённого в четвёртую степень,было наибольшим. ответ должен получится: 1 и 4

PilkaPie · Answer

Пусть одно из слагаемых равно x. Тогда второе равно 5-x. Произведение, о котором говорится в условии задается формулой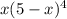 x(5-x)^4 . Нам нужно найти x, для которого это выражение оказывается наибольшим. То есть фактически нужно найти точку максимума функции 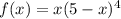f(x)=x(5-x)^4 на интервале (0; 5).

Возьмём производную:

f'(x)=(5-x)^4-4(5-x)^3=(5-x)^3(5-x-4x)=5(5-x)^3(1-x)

На заданном интервале производная имеет единственный ноль: точку x=1. При этом: f(0)=f(5)=0, f(1)=256. Значит x=1 - точка максимума на интервале (0; 5).

1 это первое слагаемое. Тогда второе, очевидно, равно 4.

ответ: 1 и 4

Популярные вопросы