решить через Дискриминант
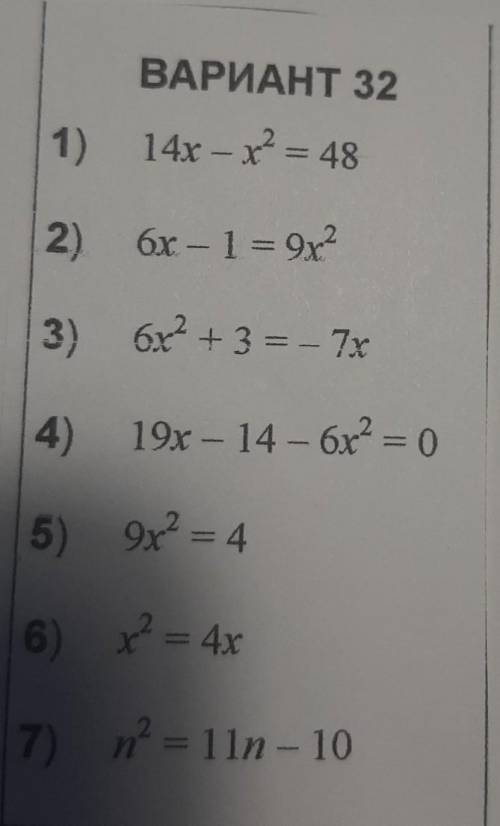
Другие вопросы по теме Алгебра
Популярные вопросы
- Для полного сгорания 13,6 г алкадиена было израсходовано 44,8 г кислорода....
2 - Свеча стоит на расстоянии 62.5 см от экрана. на каком расстоянии от свечи...
2 - Втреугольнике abc сторона ac продолжена за точку c на длину ce=cb и за точку...
2 - 5в степени 2/3 * 3 в степени 7/3 разделить это всё на 5 в степени - 1/3...
2 - 1. наклонная, проведенная из точки к плоскости, равна 10 см и образует со...
3 - Охарактеризовать реформы петра 1 в области науки и просвещения...
2 - Какие определения являются однородными а какие неоднородными? какие слова...
2 - Почему после употребления богатой белками пищи дольше не чувствуется голод,чем...
2 - Сразбавленной серной кислотой не взаимодействует: а) железо б) никель в)платина...
1 - Нужно сократить дробь: x^3+2x^2-16x-32 разделить на (x-1)^5+(1-x)^5+(x-1)^2-9...
3
В данном уравнении у нас есть три коэффициента:
a = 2
b = -7
c = -5
Дискриминант (D) вычисляется по формуле D = b^2 - 4ac. Давайте вычислим его значения:
D = (-7)^2 - 4 * 2 * (-5)
D = 49 + 40
D = 89
Теперь, когда мы знаем значение дискриминанта, мы можем делать выводы о количестве и характере корней.
1. Если D > 0, то у уравнения есть два различных корня.
2. Если D = 0, то у уравнения есть один корень (корень является двойным).
3. Если D < 0, то у уравнения нет рациональных корней (корни являются комплексными числами).
В данном случае, D = 89, что больше нуля, поэтому у нас есть два различных корня.
Чтобы найти эти корни, мы используем формулу x = (-b ± √D) / (2a).
Теперь подставим значения в формулу:
x₁ = (-(-7) + √89) / (2*2)
x₁ = (7 + √89) / 4
x₂ = (-(-7) - √89) / (2*2)
x₂ = (7 - √89) / 4
Таким образом, уравнение имеет два корня:
x₁ = (7 + √89) / 4
x₂ = (7 - √89) / 4
Это является окончательным ответом на задачу.