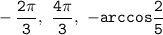Решить! а) решите уравнение (10 cos^2 + cosx - 2) / (√-sinx) = 0 б) найдите все корни этого уравнения, принадлежащие промежутку ( -π ; 3π/2)
Другие вопросы по теме Алгебра
Популярные вопросы
- это кавказкий пленник ответить на вопромы 1. С какой целбю автор так подробно...
3 - ХИМИЯ Безводный хлорид меди смешали с дигидратом хлорида меди (II) так, чтобы...
2 - Сдать, ь, хотеть,mujer1. Прочитайте и перепишите тексты. Укажите глаголы в...
3 - Сума двох чисел дорівнює 346, причому 1 число більше від 2 на 30. знайдіть...
1 - Период полураспада ядер атомов некоторого вещества составляет 24 с. Это означает,...
1 - Сколько гукав в слове ледзь...
1 - Вставтьте пропущенные слова. Тема птицы : Во время перелета большую роль играет...
3 - Ложь далась ей легко, но в душе оставив противный отпечаток. Напишите ваше...
1 - малый поршень гидравлического пресса опустился на 21 см. под действием силы...
1 - Найдите олицетворения, выпишите их из стихотворения Я.Полонского «По горам...
2
ОДЗ:
-sinx>0 ⇒ sinx<0 ⇒ x ∈ III, IV координатным четвертям (не включая концы).
Теперь отбираем корни по ОДЗ (первая картинка). Остаются две серии корней.
И напоследок отбор корней на промежутке (вторая картинка).
ответ: а)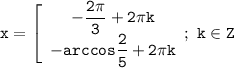 , б)
, б)