решить:) 419(в) и 422(в).
11 класс, тема: Иррациональные уравнения.
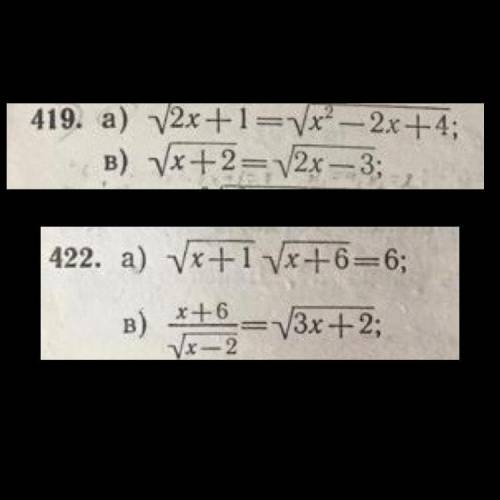
Другие вопросы по теме Алгебра
Популярные вопросы
- Алиса в стране загадок 1. Какие редкие животные живут на других планетах?...
1 - Решите уравнение 12*(икс+8)=60...
1 - Укажите один из видов невроза, который основан на преобладании подкорковой...
3 - 1.Ривера не үшін алдына жеңу мақсатын қойды?2.Шығарма неліктен «Мексика...
3 - Ex:1. Прочитать эссе и заполнить таблицу...
3 - ПТМС-поррмуласы арқылы Ы. Алтынсариннің педагогика саласындағы жаңашылдыдығы...
3 - Определить степень окисления по таблице Менделеева: Na2S, Na3N, NaBr,...
1 - . Сила F3 - это 1) сила тяжести 2) сила трения 3) сила упругости 4)...
3 - 1.президент другої малоросійської колегіїа)М.Залізняк б)П.Калнешевський...
1 - Зкласти цікаві задачі з теми Scratch?...
1
В решении.
Объяснение:
419.
в) √х + 2 = √2х - 3
Возвести обе части в квадрат:
(√х + 2)² = (√2х - 3)²
х + 2 = 2х - 3
х - 2х = -3 - 2
-х = -5
х = 5.
Проверка путём подстановки вычисленного значения х в уравнение показала, что данное решение удовлетворяет данному уравнению.
422.
в) (х + 6)/(√х - 2) = √3х + 2
Умножить уравнение (все части) на (√х - 2), чтобы избавиться от дробного выражения:
(х + 6) = (√3х + 2)*(√х - 2)
Раскрыть скобки:
х + 6 = √(3х + 2)*(х - 2) (всё выражение под корнем)
х + 6 = √3х² - 6х + 2х - 4 (всё выражение под корнем)
х + 6 = √3х² - 4х - 4 (всё выражение под корнем)
Возвести обе части уравнения в квадрат:
(х + 6)² = (√3х² - 4х - 4)²
х² + 12х + 36 = 3х² - 4х - 4
Привести подобные члены:
х² + 12х + 36 - 3х² + 4х + 4 = 0
-2х² +16х + 40 = 0
Разделить уравнение (все части) на -2 для упрощения:
х² - 8х - 20 = 0, квадратное уравнение, ищем корни:
D=b²-4ac =64 + 80 = 144 √D=12
х₁=(-b-√D)/2a
х₁=(8 - 12)/2
х₁= -4/2
х₁= -2;
х₂=(-b+√D)/2a
х₂=(8 + 12)/2
х₂=20/2
х₂=10.
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.