1. Алгебра
  2. Решить 11:3x-1-31 25 и

Решить 11:3x-1-31
25 и указать
4:9x-11:3x-1-5
наименьшее целое
Неотрицательное число, входящее в решение.


Решить 11:3x-1-31 25 и указать 4:9x-11:3x-1-5 наименьшее целое Неотрицательное число, входящее в реш

НастяMokrik НастяMokrik    3   31.08.2020 17:28    0

Ответы
154Dance3 154Dance3  15.10.2020 16:30

Замена переменной:

3^{x}=t

t 0

тогда

3^[x-1}=3^{x}\cdot 3^{-1}=\frac{1}{3} t

9^{x}=(3^{2})^{x}=(3^{x})^{2}=t^2

Неравенство принимает вид:

\frac{\frac{11}{3}t-31}{4t^2-\frac{11}{3}t-5}\geq 5

\frac{11t-93}{12t^2-11t-15}\geq 5

\frac{11t-93}{12t^2-11t-15}-5\geq 0

\frac{11t-93-60t^2+55t+75}{12t^2-11t-15}\geq 0

\frac{60t^2-66t+18}{12t^2-11t-15}\leq 0

\frac{10t^2-11t+3}{12t^2-11t-15}\leq 0    D=121-120=1    и    D=121+720=841=29²

\frac{(2t-1)(5t-3)}{(4t+3)(3t-5)}\leq 0

Применяем метод интервалов:

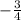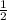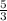___+__ (-\frac{3}{4}) ___-__ [\frac{1}{2}] __+__ [\frac{3}{5}] __-__ (\frac{5}{3}) __+__

C учетом t >0

0 < t \leq \frac{1}{2}               или        \frac{3}{5 } \leq t < \frac{5}{3}

Обратный  переход:

0 < 3^{x} \leq \frac{1}{2}              или         \frac{3}{5 } \leq 3^{x} < \frac{5}{3}

x\leq log_{3}\frac{1}{2}                или         log_{3}\frac{3}{5 } \leq x < log_{3}\frac{5}{3}

x\leq -1                     или         x=0

О т в е т.  x=0 -наименьшее целое неотрицательное

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
iobolenkov iobolenkov  01.09.2019 06:00
Решить! знак * это значит в квадрате. за ранее большое ! 7•(1/7)*-15•1/7...
ibraimova2 ibraimova2  01.09.2019 06:00
Изобразите график функции y=x^2 на множестве [-2; 1]...
ГолубьДеревенский ГолубьДеревенский  01.09.2019 06:00
Розв яжіть рівняння 2х(х+2)-9=(х-3)(х+3)...
думайй думайй  01.09.2019 06:00
Запишите величины 0,0636x10^-5 в стандартном виде....
aman1382 aman1382  01.09.2019 06:00
За 2ч. по течению и 1.5 часа против течения лодка проходит 55 км. а за 30 мин. по течению и 2 часа против течения - 30 км. найти vсобственное и vтечения. (решить системой)...
azavidov00 azavidov00  01.09.2019 06:00
Решите систему неравенств 5x+13 меньше или равно 0 и x+5 больше или равно 1...
Alina2007271 Alina2007271  01.09.2019 06:00
При каких значениях к уравнение кх²+2·(к+1)·х+к+3=0 имеет два различных корня? решите ,...
Енотик83 Енотик83  01.09.2019 06:00
Выражение 1. x^2y^2-9y^2 2.4x^3y-xy^3...
Арсений4455 Арсений4455  01.09.2019 06:00
Решить: изобразить график функции заданной формулы и указать свойства *x^2+2...
aziko2002 aziko2002  01.09.2019 06:00
Найдите разность многочленов 13y-x и 15x-3y...

Популярные вопросы