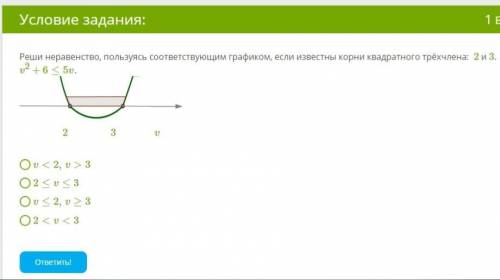
Реши неравенство, пользуясь соответствующим графиком, если известны корни квадратного трёхчлена: 2 и 3. v2+6≤5v.

Добрый день! Для того чтобы решить данное неравенство, мы можем использовать полученный график.

1. Начнем с того, что у нас есть корни квадратного трехчлена: 2 и 3. Из этого мы можем сделать вывод, что график данного трехчлена пересекает ось абсцисс (ось x) в точках 2 и 3.

2. Возьмем каждый из этих корней и отразим их относительно оси абсцисс, чтобы найти те точки, где трехчлен пересекает ось ординат (ось y). Получим точку (-2,0) и (-3,0).

3. Теперь посмотрим на неравенство: v^2 + 6 ≤ 5v. На графике выделена область, где кривая трехчлена ниже прямой y = 5x.

4. Чтобы найти значения переменной v, для которых выполняется данное неравенство, достаточно найти те точки, где кривая трехчлена находится под прямой y = 5x.

5. Проведем горизонтальную линию y = 6, которая пересекает график в двух точках. Для наглядности обозначим эти точки A и B.

6. Пересечение прямой y = 5x и горизонтальной линии y = 6 находится в точке C. Эта точка является решением неравенства.

7. Для определения точного значения этой точки, найдем уравнение прямой, и используем его для решения системы уравнений с уравнением трехчлена.

8. Уравнение прямой y = 5x имеет вид: y = 5x + 0. Заменим y в уравнении трехчлена на 5x + 0.

9. Получим следующее уравнение: v^2 + 6 ≤ 5v.

10. Перепишем это уравнение в виде: v^2 - 5v + 6 ≤ 0.

11. Для решения этого уравнения, мы можем факторизовать квадратный трехчлен. Так как у нас есть корни, то можно предположить, что (v - 2)(v - 3) ≤ 0.

12. Применим основное свойство умножения: если произведение двух чисел меньше или равно нулю, то хотя бы один из множителей должен быть меньше или равен нулю.

13. Получим два набора условий: (v - 2) ≤ 0 и (v - 3) ≤ 0. Каждое из них будет представлять собой отдельное неравенство.

14. Решим первое неравенство (v - 2) ≤ 0. Для этого добавим 2 ко всем частям неравенства: v ≤ 2.

15. Решим второе неравенство (v - 3) ≤ 0. Для этого добавим 3 ко всем частям неравенства: v ≤ 3.

16. Теперь, используя оба набора условий, мы можем записать решение исходного неравенства: v ≤ 2 и v ≤ 3.

17. Объединяя эти два условия, мы можем записать ответ в виде: v ≤ 2.

Таким образом, решением данного неравенства является множество всех значений v, меньших или равных 2.