Решение логарифмических уравнений.
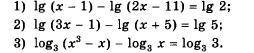
Другие вопросы по теме Алгебра
Популярные вопросы
- 50 . влияние популяризации на побуждение к мотивации занятию сноубордингом....
2 - X-(500+79)=221 pomogite reshi...
2 - 4и 5 вопрос стр.16 и 1 вопрос стр.17 ! 20 ....
1 - Эссе на тему защитим наши почки коротко...
2 - Какие товарищества в военном отношении и структуре полков использовал...
3 - Опишите изменения в по каждой из указанных отраслей (не менее 2-х...
3 - Пути движения автомашины 4 светофора, каждый из которых запрещает...
2 - Правильное ли зто предложение while i watched it my grandma phoned...
2 - Вобщем, нужно используя функции mod и div составить программу по...
2 - Составьте предложения с предлогами: в случае; в следствие; при отсутсвии;...
3
lg(x-1)-lg(2x-11)=lg2
ответ:7
2.lg(3x-1)-lg(x+5)=lg5
ответ:-13
3.x=0
x=±2
ответ:2