Ребят с алгеброй. а то дома сижу больной не знаю как это делать.
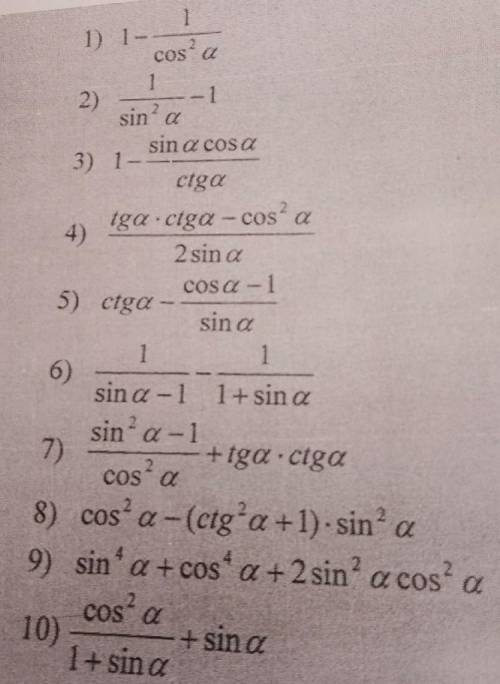
Другие вопросы по теме Алгебра
Популярные вопросы
- Сочинение на тему роль случая в повести барашня крестьянка ...
3 - В магазин привезли несколько упаковок карандашей по 12 штук в каждой упаковке...
1 - Презентация на тему дефицит макроэлементов азота калия и фосфора в минеральных...
2 - Хэлп ми P. S. Перед тем как писать ответ сначала посмотрите на кроссворд выше,...
1 - Элемент, который образует ион с зарядом Э2-, присоединяет электроны на третий...
1 - Какая из реакций является окислительно-восстановительной и почему? Для окислительно-восстановительной...
1 - Задание 100 1. Прочитайте текст, состаньте вопросный план.2. Выпишите термины...
1 - Юля хочет сделать цветочную клумбу в форме параллелограмма у неё есть 14, 6м декоративного...
1 - Суретте не бейнеленген? Қалай ойлайсың, бұл не? Қандай мақсатта дайындалған? Қазақ...
3 - Казак адеб тжб онлайн мектеп у кого есть...
3
решение смотри на фотографии
Объяснение:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.