разобраться с тригонометрическим уравнением: 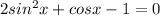 В задании был ответ: ±
В задании был ответ: ± 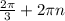 , n ∈ Z.
, n ∈ Z.
Это уравнение я решил так:
или 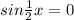
, n∈Z или 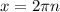 , n∈Z
, n∈Z
в итоге ответ у меня получился 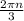 , n∈ Z.
, n∈ Z.
Правильное ли мое решение? ответ 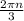 , n∈ Z и ±
, n∈ Z и ±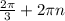 , n ∈ Z это одно и тоже?
, n ∈ Z это одно и тоже?
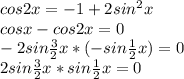
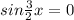
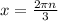
Ответы
Показать ответы (3)
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. В шахту спускается груз массой 50кг и в первые 15с от начала равноускоренного...
1 - Знайти опір баратеї резисторів. Відповідь заокруглити до десятих. Дано:...
3 - Чи припинив свою діяльність Малишко під час Другої світової війни?...
3 - Решите контрольная работа, очень Решите контрольная работа, очень...
3 - 6. Поширену обставину потрібно відокремити комою в реченні(розділові...
1 - VI. Wäsche waschen. Ergänzen Sie die Sätze mit den Verben im Infinitiv....
2 - Письменно ответить на во опираясь на текст произведения железникова...
3 - с тестом (доделать часть 1) 11. При человека к новым для него условиям...
3 - 10. Кому між виділеними сполучниками треба поставити в реченніA Сині...
3 - Квадрат суммы выражений 2а и 3с равен в квадрате плюс · · плюс в квадрате....
3