1. Алгебра
  2. , разложите на множители: 4x^4-4x^2+4x-1

,
разложите на множители: 4x^4-4x^2+4x-1

evamayninger20 evamayninger20    2   01.08.2022 16:07    0

Ответы
KaFnaTou KaFnaTou  01.08.2022 16:08
4x⁴-4x²+4x-1=4х⁴-(2х-1)²=(2х²)²-(2х-1)²==(2х²+(2х-1))(2х²-(2х-1))=(2х²+2х-1)(2х²-2х+1)
ПОКАЗАТЬ ОТВЕТЫ
Яумницакрасотка Яумницакрасотка  01.08.2022 16:08

\frac{1}{2}(2{x^2} - 2x + 1)(2x - \sqrt 3 + 1)(2x + \sqrt 3 + 1)

Объяснение:

4{x^4} - 4{x^2} + 4x - 1 = 4{x^4} - (4{x^2} - 4x + 1) = \\={(2{x^2})^2} - {(2x - 1)^2} = (2{x^2} - 2x + 1)(2{x^2} + 2x - 1).

Так как дискриминант трехчлена в первых скобках отрицателен, она не раскладывается на множители.

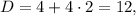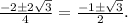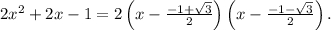
Рассмотрим трехчлен во второй скобке. Его дискриминант D = 4 + 4 \cdot 2 = 12, потому корни \frac{{ - 2 \pm 2\sqrt 3 }}{4} = \frac{{ - 1 \pm \sqrt 3 }}{2}. Тогда 2{x^2} + 2x - 1 = 2\left( {x - \frac{{ - 1 + \sqrt 3 }}{2}} \right)\left( {x - \frac{{ - 1 - \sqrt 3 }}{2}} \right).

Окончательно, после вынесения коэффициентов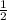 \frac{1}{2} из каждой скобки, получаем

4{x^4} - 4{x^2} + 4x - 1 = \frac{1}{2}(2{x^2} - 2x + 1)(2x - \sqrt 3 + 1)(2x + \sqrt 3 + 1).

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Deiselpro1 Deiselpro1  06.05.2020 11:52
Прямая y=kx+b проходит через точки A (2;-1) и B (-3;24). Запишите уравнение этой прямой...
свайпер свайпер  06.05.2020 11:52
Знайдіть суму шести перших членів арифметичної прогресії, в якої а1=-22; d=2....
bella80 bella80  06.05.2020 11:52
Желательно с объяснением ​...
pip2281 pip2281  06.05.2020 11:52
Оцініть периметр прямокутника зі сторонами a см і b см, якщо...
iprin iprin  06.05.2020 11:52
Как это решить?Система линейных уравнений...
gareevaa05 gareevaa05  06.05.2020 11:52
Найдите значение выраженияесли а ​...
maximruba maximruba  06.05.2020 11:52
Точка В на прямій лежить між точками А і С АС=18 см , ВС=10 см , тоді АВ дорівнює А-28см Б-14см В-8см Г-4см допомржіть...
natashaevtushenko natashaevtushenko  06.05.2020 11:52
Сколько целых чисел принадлежит промежутку: (−9;5)?​...
betmen654 betmen654  06.05.2020 11:52
Які з пар чисел є розв’язком системи рівнянь з двома змінними x+y=7 x-y=3 а) х= 3; у= 4 ; б) х= 5; у= 2; в) х= 6; у= 3....
20AKE04 20AKE04  06.05.2020 11:52
Принадлежит ли промежутку (−7;7) число −0,4?​...

Популярные вопросы