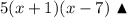Разложить на множители 5x^2-30x-35
Другие вопросы по теме Алгебра
Популярные вопросы
- Олег и игорь живут на разных концах улицы строителей они ходят в школу которая...
1 - 1. укажите номера, под которыми перечислены главные члены предложения: 1) подлежащее.2)...
1 - Выражения 1)17х+4х-15+30 2)19х-7+10х+1...
2 - Как будет на хорошо как дела че делаешь бомба молодец сколько лет...
3 - Решите ((21,85: 43,7+8,5: 3,4): 4,5): 1+1=...
1 - Докажите с схем, докажите что в данных текстах сочетаются разндокажите с схем,...
2 - Перевести на язык, употребляя глаголы в необходимых временах группы perfect....
2 - Какая скорость больше: 10.0 м/с или 38 км/ч; 32.0 м/с или 110 км/ч...
2 - Какие органоиды клетки имеют двумембранное строение: а)митохондрии,хлоропласты...
3 - 1. дано натуральное число а. если а - четное, то вывести косинус числа а и квадратный...
3
Чтобы разложить квадратный трехчлен на множители, нужно воспользоваться схемой:
на множители, нужно воспользоваться схемой:
Здесь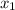 и
и 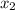 — корни квадратного уравнения
— корни квадратного уравнения 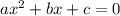
Решим уравнение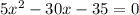 по теореме Виета.
по теореме Виета.
Разделим обе части уравнения на 5:
Таким образом,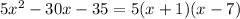
ответ: