Равнобокая трапеция с основаниями 9 см и 16 см описана около окружности. найдите радиус окружности. С черчежом. Кто обманет БАН

r=3.

Объяснение:

1) Так как трапеция ABCD равнобокая и в неё вписана окружность, то её боковые стороны будут равны средней линии трапеции, т.е. AB=CD=m, где m===12,5. ⇒ AB=CD=12,5.

2) Проведём из точек В и С перпендикуляры к стороне AD. ⇒ BH₁=CH ⇒ AH₁=HD=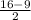=3,5.

3) Рассмотрим прямоугольный треугольник ABH₁. И по теореме Пифагора найдём высоту трапеции ABCD, т.е. BH₁. ⇒

⇒ BH₁===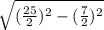==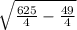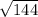12.

4) Площадь трапеции равна S=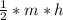, где m - сред.линия; h - высота трапеции. ⇒ S=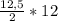=6,25*12=75.

5) Так как в трапецию вписана окружность, то её площадь равна S=pr, где p - полупериметр трапеции; r - радиус вписанной окружности.

⇒ p=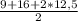=25. ⇒ 75=25*r ⇒ r=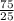=3.