Расстояние между поселками А и В равно s км. Из А отправились в В одновременно по одной и той же дороге два автотуриста, которые должны были прибыть в В в одно и то же время. В действительности первый турист прибыл в В на n ч раньше срока, а второй на 3n ч опоздал, так как последний проезжал за каждый час в среднем на r км меньше первого. Определить среднюю скорость каждого автотуриста. Не знаю 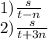$1) \frac{s}{t - n} \\2) \frac{s}{t + 3n}$ куда r деть

Ответы

078901234567 08.08.2021 06:00

Средняя скорость первого туриста:

r/2 + √((r²/4) +sr/4n);

Средняя скорость второго туриста:

- (r/2 - √((r²/4) +sr/4n))

Объяснение:

Пусть х и у - скорости движения первого и второго туристов, а t - время их движения, если бы они шли с одинаковой скоростью, тогда:

s/x = t-n - фактическое время движение первого туриста, (1)

s/y = t+3n - фактическое время движения второго туриста. (2)

Из второго уравнения вычтем первое:

s/y - s/x = t+3n - (t-n)

s/y - s/x = t+3n - t+n

s(1/y - 1/x) = 4n

s[(х-у)/ху] = 4n (3)

так как (х-у) = r (согласно условию), (4)

то подставим (4) в (3):

sr/ху = 4n

ху = sr/4n (5).

Согласно теореме Виета, сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а их произведение равно свободному члену.

Обозначим переменную v.

Тогда приведённое квадратное уравнение c учетом (4) и (5) имеет вид:

v² - rv - sr/4n = 0, (6)

так как

х + (-у) = r

х· (-у) = - sr/4n.

Соответственно скорости равны:

v₁ = х = r/2 + √((r²/4) +sr/4n)

v₂ = - y = - (r/2 - √((r²/4) +sr/4n))

ответ: средняя скорость первого туриста:

r/2 + √((r²/4) +sr/4n);

средняя скорость второго туриста: