Распишите подробно решение неравенства
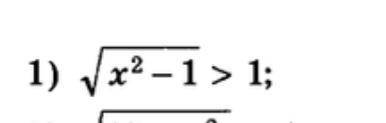
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему корабли, сделанные из железа не тонут? потскажите!...
3 - Может ли человек иметь массу 82000 г ,рост 1920мм? ответ пояснить....
3 - Какие цифры должны стоять вместо * чтобы вычисления лики стали верными?...
1 - Вычисли значение выражения.32*(645: 15*18+226)-100: (75: 3)...
3 - Однородными сказуемыми осложнено предложение а)дни стояли теплые...
3 - Правило включение амперметра и вольтметра в цепь!...
2 - Опишите опыт ньютона по разложению белого света в спектр...
3 - Какой падеж в предложении сойка прячет их на зиму...
1 - Сделай предложения отрицательными. 1) her hair was long last year.-...
2 - Сделать звуко-буквенный разбор слова (заря)...
1
ОДЗ:
х принадлежит (-беск;-1]U[1;+беск).
Возведем обе части во 2 степень:
х принадлежит
Пересекаем с ОДЗ и получаем ответ:
х принадлежит