1. Алгебра
  2. Радиус основания конуса увеличили

Радиус основания конуса увеличили в 2 раза,а высоту - в 3 раза. во сколько раз увеличился объём конуса?

ipolevoy1 ipolevoy1    1   27.09.2019 02:00    2

Ответы
dkurmanbek dkurmanbek  08.10.2020 21:39

Пусть новый радиус основания равно R*, а новая высота - h*. Согласно условию r=2R* и h = 3h*.


Объем конуса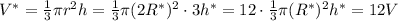 V^*=\frac{1}{3} \pi r^2h=\frac{1}{3} \pi (2R^*)^2\cdot 3h^*=12\cdot \frac{1}{3} \pi (R^*)^2h^*=12V


\displaystyle \frac{V^*}{V} =12, где V* - новый объем и V - изначальный объем

в 12 раз увеличился объём конуса.

ПОКАЗАТЬ ОТВЕТЫ
maksatovna17 maksatovna17  08.10.2020 21:39

Фoрмула объема конуса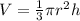 V=\frac{1}{3} \pi r^{2} h\\, где r - радиус основания, а h - высота.


Видно чо если высота увеличилась в 3 раза, значит и объем увеличивается в 3 раза. Но радиус берется в квадрате, значит надо брать 2 в квадрате, то есть 4. В итоге объем конуса увеличиваетса 3*4= 12 (раз).

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
172839465 172839465  13.04.2020 20:01
На рисунке построенв графики уравнений. Запишите соответствующую систему уравнений и укажите ее решение​...
vladimirova2002 vladimirova2002  13.04.2020 18:29
Функция задано формулой у = -2,5х + 3,4.Добавить точку, которая принадлежит графику этой функции.Варианты ответов:(0; 3,4)(2; -1,6)(3,4; 0)(-2, 1,6)​...
Pandochkalove7 Pandochkalove7  13.04.2020 18:29
Выполните умножение многочленов (0,4a+0,5)(0,4-0,5)...
умный2006 умный2006  08.04.2020 14:49
У прямоугольного параллелепипеда стороны основания равны 8 см и 5 см, а боковая поверхность — 364 см2. Определи высоту H прямоугольного параллелепипеда. ответ: H = см...
sabina1705 sabina1705  08.04.2020 14:49
Розв яжіть систему рівнянь графічно ​...
соня1571 соня1571  08.04.2020 14:49
1. Дана таблица распределения частот использования терминала банкомата в одном торговом центре по дням недели. Найдите накопленную частоту.Дни недели Понедельник Вторник Среда Четверг...
Lena2402bux Lena2402bux  08.04.2020 14:49
Решите неравенства и изобразите множество его решений на координатной прямой а) 11x -33; б)-8 ≥ 24 ; в)-6 -12 г) 13x ≤ -65....
Kseiaa Kseiaa  16.11.2019 08:44
Объясните тему линейные ыункции...
топтип топтип  16.11.2019 08:30
[25 б.] что бы я не делал у меня получается 36, но в ответе написано 30. , ​...
amina090806 amina090806  13.08.2019 16:30
Как доказать тождество (а+в)в квадрате = а в квадрате + 2ав+в в квадрате...

Популярные вопросы