Радиоуправляемый корабль и бревно одновременно отплыли вниз по реке. Проплыв 8 км, корабль понял, что его батареи разряжаются, развернулся и пошел вверх по реке. Проплыв 6 км, он встретился с бревном. Какова собственная скорость корабля, если скорость течения реки 4 км/ч?ответ выразите в км/ч.

Сразу обозначим собственную скорость корабля за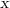 . Тогда:

Заметим, что за то время, пока корабль успел проплыть туда-сюда, бревно лишь проплыло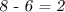 км со скоростью км/ч (за скорость бревна мы принимаем скорость реки, так как подразумеваем, что никаких людей или моторчика на бревне не предусмотрено).

Значит, время движения бревна равно часов.

И еще:

Так как бревно и корабль двигались одинаковое время, то мы можем дальше только составить уравнение и решить его:

Первый корень не сказать, чтобы нам подходит, а второй корень - в самый раз! Он не только правдоподобный, но и не дает нуля в знаменателе!

Задача решена!