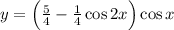Пусть y(x) - решение задачи Коши y′–ytgx=sinx, y(0)=1. Найти y(π)
Другие вопросы по теме Алгебра
Популярные вопросы
- Смешали 4 литра горячей воды при температуре 60 с и 2 литра холодной...
2 - 30 б. ! нужно составить 6 диалогов. тема : дружба (о дружбе)...
1 - Главное слово словосочетания общественно необходимый...
3 - Tell your friend about the most interesting holiday in america...
1 - Al+hcl=alcl3+h2 где окислитель а где восстановители...
1 - Путешественник в первый день всего пути,во второй день остальной...
3 - Составь из слов предложения. в конце поставь нужный знак. над выделенными...
1 - Взаимосвязь естественных наук в исследовании воды?...
2 - Название пословицы кто грамоте горазд-тому не пропасть объяснить...
2 - What tense should be used if the sebtence has one of these words?...
1
Домножаем к левой и правой частям дифференциального уравнения на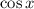 , имеем
, имеем  . Левую часть уравнения можно представить в виде:
. Левую часть уравнения можно представить в виде:
Замечаем, что левая часть последнего диф. уравнения это дифференцирование произведения двух функций и в правой части применяем синус двойного угла.
Осталось найти частное решение, подставив начальные условия
Частное решение данного диф. уравнения: