Пусть (x1) и (x2) - корни уравнения 4x^2-6x-1=0. Составьте квадратное уравнение, корнями которого являются число (y1)=(2/(x1)^3)-1
(y2)=(2/(x2)^3)-1
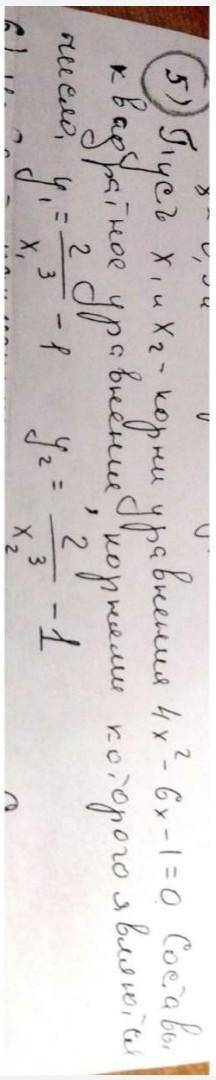
Другие вопросы по теме Алгебра
Популярные вопросы
- треугольник АВС и КМN, угол А равен углу К, АС=5см, АВ=5см, КМ=2см,...
1 - русский язык сор 3 задание класс7...
1 - Функции5. Определить угловой коэффициент и свободный член...
1 - Где в россии самая холодная зима...
2 - Дать характеристику одной из трех стран по плану Индия Китай и Япония...
1 - При горении метана выделяется 892 кДж тепла. Подсчитайте количество...
1 - Длина прямоугольника равна 3,1/12см, а ширина на 3,1/2 больше длины,...
3 - 2. Используя переместительное и сочетательное свойства, вычисли...
2 - Напишите выражение закона действующих масс для реакции: Ι. 2NO(г)...
3 - Нужно найти деепричастный оборот и просто деепричастия и выделить...
1
1)
По теореме Виета для уравнения 4х²-6х-1 :
х1+х2 = 1.5
х1*х2 = -0.25
2)
По теореме Виета для нового уравнения :
В = -(у1+у2) = -((2/х1³)-1 +(2/х2³)-1) = 578
С = -(у1*у2) = ((2/х1³)-1)*((2/х2³)-1) = 321
Уравнение : y²+578y+321 = 0
ответ : у²+578у+321 = 0
P.S если интересно как я из -((2/х1³)-1 +(2/х2³)-1) получил 578, то я сейчас примерно покажу (для удобства пусть х1 будет х, а х2 будет у) :
Ну и уже по теореме Виета (х+у = 1.5, х*у = -0.25) я подставил значения и решил, с умножением там примерно тоже самое)
Объяснение: см. во вложение