Прямая y=ax+b перпендикулярна прямой у=0,5х-4 и проходит через точку с(2; 6) . составьте ее уравнение
Другие вопросы по теме Алгебра
Популярные вопросы
- Сколько молей марганца содержится в 220г марганца...
3 - Охарактеризуйте капітана макака і яку йому дати пораду?...
3 - Найдите значение выражения (3-4) 144: (12*11-108)....
2 - Морфологический разбор слова камышовая...
1 - 1836: (26-4у)=102 3216: (5у-102)=16 нужно найти 5у и 4у с пояснением...
3 - Главная мысыль в рассказе о сурове и садотов...
1 - 3x+5=10 10у+2=7 8x+6=12 7x+8=0 2x+7=-20 решите...
1 - Вкажіть значення слизу ,що виділяється шкірними залозами амфібій: а) полегшує...
1 - Даны точки а(-1; 3) в(11; -20) с(3; 2) d(12; -3). какая из 6 прямых ab dc...
1 - Найти неизвестный член пропорции x/10=1,3/1,5...
3
Пряммую будем искать в виде y=kx+b
из условия перпендикулярности прямых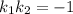 получаем, что угловой коэфициент
получаем, что угловой коэфициент 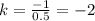
Искомая пряммая проходит через точку С(2;6), значит справедливо равенство
y=kx+b;
6=-2*2+b;
из которого
b=6+2*2=6+4=10
значит искомое уравнение y=-2x+10
условие перпенджикулярности a1*a2=-1
a*0.5=-1
a=-2
y=-2x+b
C(2.6) -2*2+b=6 b=10
y=-2x+10