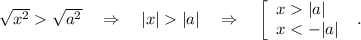прояснить один момент в примере. На первом скриншоте дан сам пример.
На втором же предоставлено решение и разъяснение.
Так вот, можете более простым языком прояснить момент с написанием ответа. Что это за условие |x| > |a| и почему именно оно. И как потом считается ответ.
не совсем понятен этот момент.
С самим решением можно сказать разобрался, сложность возникает именно в этих модулях и условиях.
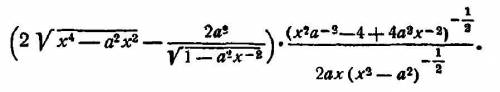

Другие вопросы по теме Алгебра
Популярные вопросы
- Запобігання ескалації конфліктів. Самоконтроль1. Знайди та обведи...
1 - Read and write. Invent your own city tour. My city tourMy city...
1 - Как жизнь Алеши в доме бабушки и дедушки повлияла на его характер.Произведение...
3 - U=100sin(wt+П/2) Визначте вираз струму якщо опiр кола 100 Ом, i...
3 - Диагонали AC и BD трапеции ABCD с основаниями ВС и AD пересекаются...
1 - Прочитайте приведенный ниже текст. Преобразуйте слова в скобках...
3 - үтірдің қойылатын орындарына байланысты қазіргі әлемдік саясат...
2 - Яку риси обличчя маленький івасик успадкував від батька та матері...
3 - 5. Страдательное причастие времени нельзя образо от глаголаА) сломатьВ)...
3 - Here are the words but the letters are mixed up. Write the correct...
2
бьответ:
Дробь в числителе имеет неотрицательное выражение при любом "х" , то есть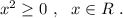 Тогда, чтобы вся дробь была неотрицательной, надо, чтобы знаменатель был положительным ( нулю равняться он не может), то есть необходимо, чтобы выполнялось неравенство:
Тогда, чтобы вся дробь была неотрицательной, надо, чтобы знаменатель был положительным ( нулю равняться он не может), то есть необходимо, чтобы выполнялось неравенство:
Чтобы определить , каким должен быть "х" , надо извлечь квадратный корень из обеих частей неравенства. Известно правило извлечения корней из квадрата какого-либо выражения: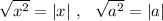 .
.
Поэтому