Провести полное исследование указанных функций и построить их график
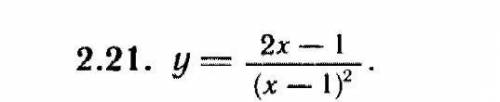
Другие вопросы по теме Алгебра
Популярные вопросы
- Сила тяжести,которая действует на некое тело,равна 10 кн. какова...
2 - Зелёная падеж: иминительный: число: ед.ч.: род: женский...
1 - :какую роль в атмосфере играют кислород, азот, углекислый газ и...
3 - На пошив одного платья и одного халата портной потратил одинаковое...
3 - Текст-рассуждение на тему что такое совесть? 4 класс (из интернета...
2 - Замените словосочетание «книжная полка»(предложение 18), построенное...
1 - Ученики пятого класса писали контрольную работу 1/6 учеников класса...
3 - Одень день з життя середньорічної герцогині.(что делала в сколько...
1 - 8кг290г – 4кг370г 24м67см - 12м89см 3км276м+6км938м 6кг380г – 2кг450г...
3 - Может ли высота треугольника быть меньше любой из его сторон...
3
Пересечение с осью x:
Пошаговое решение:
Пересечение с осью y:
Пошаговое решение:
Облость определения:
Пошаговое решение:
Производная:
Пошаговое решение:
Точка перегиба:
Пошаговое решение:
В нет точки перегиба
нет точки перегиба
График: