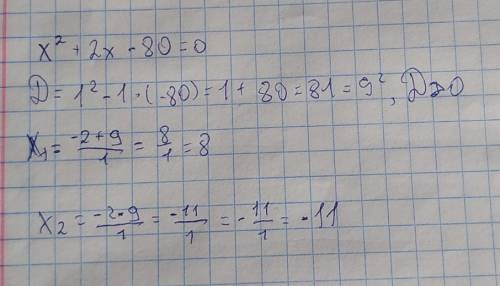
Алгебра: Проверьте ответ должен получиться 8; и -10.

8 и -10Объяснение:Неправильно найден дискриминант:D=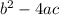 D=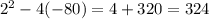 Вообще проще посчитать по теореме Виета, где:х1+х2= -b = -2 x1= - 10x1 * x2 = c = - 80 x2= 8 ...

Проверьте ответ должен получиться 8; и -10.

Ответы

rashas05 15.10.2020 15:11

8 и -10

Объяснение:

Неправильно найден дискриминант:

D= $b^{2} -4ac$

D= $2^{2} - 4(-80)= 4+320=324$

$\sqrt{D} =18$

Вообще проще посчитать по теореме Виета, где:

х1+х2= -b = -2 x1= - 10

x1 * x2 = c = - 80 x2= 8

ПОКАЗАТЬ ОТВЕТЫ

Quickfast77 15.10.2020 15:11

1. Найдём дискриминант данного уравнения.

Наше уравнение вида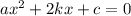 $a{x}^{2}+2kx+c=0$ , значит будет проще найти дискриминант по 2 формуле: 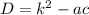$D={k}^{2}-ac$ (где k=a=1 , c=-80 ).

$D={1}^{2}-1\cdot(-80)=1-(-80)=1+80=81$ 2. Определим кол-во корней в уравнении.

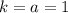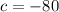Вспоминаем правила дискриминанта:

Если дискриминант больше нуля, то уравнение имеет 2 корня.Если дискриминант меньше нуля, то уравнение не имеет корней.Если дискриминант равен нулю, то уравнение имеет 1 корень.

Найденный дискриминант больше нуля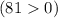 (810) , поэтому данное уравнение имеет 2 корня.

3. Найдём определённое кол-во корней уравнения.

Формула корня(-ей) такова: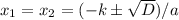 ${x}_{1}={x}_{2}=(-k\pm \sqrt{D})/a$

(где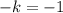 -k=-1 , D=81 , a=1 ).

${x}_{1}=(-1-\sqrt{81})/1=(-1-9)/1=\Big(-(1+9)\Big)/1=(-10)/1=-10$ ${x}_{2}=(-1+\sqrt{81})/1=(-1+9)/1=\Big(-(1-9)\Big)/1=8/1=8$ 4. Запишем окончательный ответ:

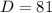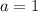Корни данного уравнения: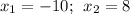 ${x}_{1}=-10; \: \: {x}_{2}=8$ .