1. Алгебра
  2. Проверить, удовлетворяет ли указанному

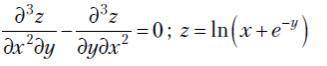
Проверить, удовлетворяет ли указанному уравнению с частными производными данная функция.


Проверить, удовлетворяет ли указанному уравнению с частными производными данная функция.

JelliTD JelliTD    3   28.06.2020 14:17    4

Ответы
danilcapitan danilcapitan  15.10.2020 15:01

z=ln(x+e^{-y})\\\\\dfrac{\partial z}{\partial x}=\dfrac{1}{x+e^{-y}}\ \ \ ,\ \ \ \ \dfrac{\partial ^2z}{\partial x^2}=\dfrac{-1}{(x+e^{-y})^2}\\\\\\\dfrac{\partial ^3z}{\partial x^2\partial y}=\dfrac{2(x+e^{-y})\cdot e^{-y}\cdot (-1)}{(x+e^{-y})^4}=-\dfrac{2\cdot e^{-y}}{(x+e^{-y})^3}

\dfrac{\partial z}{\partial y}=\dfrac{-e^{-y}}{x+e^{-y}}\ \ \ ,\ \ \ \dfrac{\partial ^2z}{\partial y\partial x}=\dfrac{-(-e^{-y})\cdot 1}{(x+e^{-y})^2}=\dfrac{e^{-y}}{(x+e^{-y})^2}\\\\\\\dfrac{\partial ^3z}{\partial y\partial x^2}=\dfrac{-e^{-y}\cdot 2(x+e^{-y})}{(x+e^{-y})^4}=-\dfrac{2\cdot e^{-y}}{(x+e^{-y})^3}

\dfrac{\partial ^3z}{\partial x^2\partial y}-\dfrac{\partial ^3z}{\partial y\partial x^2}=-\dfrac{2e^{-y}}{(x+e^{-y})^3}+\dfrac{2e^{-y}}{(x+e^{-y})^3}=0\\\\\\\star \ \ (lnu)'=\dfrac{u'}{u}\ \ ,\ \ \ \ \Big(\dfrac{C}{u}\Big)'=\dfrac{-C\cdot u'}{u^2}\ \ \star

ПОКАЗАТЬ ОТВЕТЫ
DaiDZ DaiDZ  15.10.2020 15:01

z=ln(x+e^(-y))

dz/dx=1/(x+e^(-y))*(x+e^(-y))'=1/(x+e^(-y))

d2z/dx2=((x+e^(-y))^(-1))'=-(x+e^(-y))^(-2)*(x+e^(-y))'=-1/(x+e^(-y))^2

d3z/dx2dy=(-(x+e^(-y))^(-2))'=-(-2(x+e^(-y)))^(-3)*(x+e^(-y))'=2(x+e^(-y))^(-3)*(-e^(-y))=-2e^(-y)/(x+e^(-y))^3

dz/dy=1/(x+e^(-y))*(x+e^(-y))'=1/(x+e^(-y))*(-e^(-y))=-e^(-y)/(x+e^(-y))

d2z/dydx=(-e^(-y)*(x+e^(-y))^(-1))'=-e^(-y)*((x+e^(-y))^(-1))'=

-e^(-y)*(-((x+e^(-y))^(-2)))*(x+e^(-y))'=e^(-y)/(x+e^(-y))^2

d3z/dydx2=(e^(-y)/(x+e^(-y))^2)'=e^(-y)((x+e^(-y))^(-2))'=

e^(-y)*(-2((x+e^(-y))^(-3)))*(x+e^(-y))'=-2e^(-y)/(x+e^(-y))^3

и все

-2e^(-y)/(x+e^(-y))^3-(-2e^(-y)/(x+e^(-y))^3)=-2e^(-y)/(x+e^(-y))^3+2e^(-y)/(x+e^(-y))^3=0

Объяснение:

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
homonorolla homonorolla  19.07.2019 06:00
√x+21 - √4x+3 = 0 как решить...
kislayaya13 kislayaya13  19.07.2019 06:00
Решите уравнения: a) (5-p)/(6p)=-1 b) (-2p)/(2p-6)=2...
semkin2004p0ds7g semkin2004p0ds7g  13.05.2021 11:04
Обчисліть похідну та її значення в т. Xof(x)=x2 +4x-6 Xo=-2...
КсенияА2006 КсенияА2006  13.05.2021 11:04
При яких значеннях p і q вершина параболи y = x2 (x у квадраті ) + px + q знаходиться в точці ( -6; -43 )?...
alexa7021 alexa7021  13.05.2021 11:02
Нехай х, і х, корені рівняння *+5х-13-0. Знайти х? +х,?. (Самі корені знаходити не потрібно​...
vikioria vikioria  21.12.2020 19:10
Знайти нулі функції f(x)=x²-2x+1​...
4443468234763399 4443468234763399  11.08.2019 04:30
Докажите что выражение 122^10-122^9 кратно 11^2; 4^18+4^16 кратно 34...
8алина82 8алина82  11.08.2019 04:30
Выполняя построения найдите координаты точки пересечения графика функций y=10x+10 и y=-5x+4...
mdior10 mdior10  13.11.2020 14:49
Построй график функции у=х+3​...
Комарова23 Комарова23  13.11.2020 14:49
На рисунке изображён график квадратичной функции y=f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера.1) Функция возрастает на промежутке...

Популярные вопросы