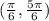Проверить справедливость теоремы Ролля для функции y=ln sin x на отрезке [pi/6;5pi/6] очень
Другие вопросы по теме Алгебра
Популярные вопросы
- Серік сезі сөзі қандай ө3. Бос торкөздерге тиісті әріптерді қойып,...
3 - Площа прямокутника зі сторонами a і b обчислюється за формулою...
1 - Історичний портрет Князя Святослава Ігоровича 1. Як відбулося...
2 - 135 упр. В каком ряду во всех слова пишется о, а в каком-ё? ...
2 - Даны точки а(-1;4) в(-2;5) найдите координаты векторов 0,3а+10в...
1 - Время появления феодализма, натурального хозяйства, новых городов....
1 - с вопросом, заранее Одним из международных последствий контрнаступления...
3 - Год появления первого персонального компьютера - .. 1990 году1950...
3 - Менің тұсау кесер тойым эссе...
2 - . Укажите неверное утверждение ) слинять - диалектизм) бить баклуши...
2
Объяснение:
Теорема Ролля утверждает.
Если вещественная функция, непрерывная на отрезке![{\displaystyle [a,b]}](/tpl/images/1464/4311/72c4a.png) и дифференцируемая на интервале
и дифференцируемая на интервале 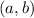 , принимает на концах отрезка
, принимает на концах отрезка ![{\displaystyle [a,b]}](/tpl/images/1464/4311/72c4a.png) одинаковые значения, то на интервале
одинаковые значения, то на интервале 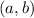 найдётся хотя бы одна точка, в которой производная функции равна нулю.
найдётся хотя бы одна точка, в которой производная функции равна нулю.
Условия теоремы выполняются, функция непрерывна и дифференцируема, на концах принимает одинаковые значения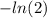
Найдем производную.
Производная обращается в ноль в точке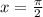 , которая принадлежит интервалу
, которая принадлежит интервалу