Прологарифмировать с основанием 2
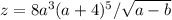
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите 28 слов с любыми орфограммами....
1 - Какие группы населения получили новые возможности для укрепления своего...
2 - :прочитайте слова и составьте предложения. великая дружба, казахстан, пример,...
3 - Перша сторона квадрата збiльшили на 4дм,а другу зменьшили на 6дм.у результатi...
2 - :в открытиях xviii века участвовали...
2 - На 6 одинаковых костюма израсходовали 24 метра ткани.сколько метров ткани...
2 - Вынесите общий множитель за скобки 14c-14*3...
3 - Проверьте все ли правильно. i prefer to spend my spare time alone. l often...
1 - Пользуясь основным свойством пропорции,проверьте, верна ли пропорция б)116/12=29/3...
3 - Как меняются главные герои романа а.с. пушкина «евгений онегин»...
2
Объяснение:
логарифм произведения/частного равен сумме/разности логарифмов, при условии, что отдельные части могут существовать
8a^3=(2a)^3=2^3*a^3
lgz=lg(2^3)+lg(a^3)+lg(a+4)^5-lg(√(a-b)),где lg- будем считать двоичным логарифмом, а не десятичным
Запишем еще свойства логарифмa loga(a)=1, loga(b)^n=n*loga(b)
3+3lga+4lg(a+4)-2,5lg(a-b) т.к. √a=a^0,5.
Ну а теперь дополнительные условия, а>0, a-b>0