. Производные Дано уравнение функции:
Определите точку ее минимума
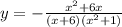
Другие вопросы по теме Алгебра
Популярные вопросы
- На съезде ассоциации (Лебедь рак и щука) в сувенирном магазине была предложена...
3 - ✨✨✨Мая мусорка! : я злая Не подходи!...
3 - 5. Сын есімдерді шырай түріне ажырат. В предложениях найдите имена прилагательные...
2 - У залізну каструлю масою 1,5 кг налито 2,5 л води за t-20°C.Скільки теплоти...
1 - ВОПРОСЫ И ЗАДАНИЯ 1. Какое влияние оказала биосфера на другие оболочки Земли?2*....
2 - 1)F(x)ctg^2x-3cos^4 3x 2)f(x)=ln x/1-x 3)f(x)=4^2x*x^4 найти производное...
1 - 1. Выполнить деление «углом». P(x) = x4 + x3 + 2x2 + x + 1 на Q(x) = x2 – x...
1 - Твердження які стосуються реформ католицької церкви...
2 - Напишіть анкету для лицаря...
3 - Біріккен сөздері бар 5 мақал-мәтелдер керек еді...
2
Объяснение:
вынесем в числителе х за скобку и сократим числитель со знаменателем на х+6
y=-x(x+6)/[(x+6)(x²+1)]=-x/(x²+1)
y'=-[x²+1-x2x]/(x²+1)²=-[x²+1-2x²]/(x²+1)²=-(-x²+1)/(x²+1)²=(x²-1)/(x²+1)²
y'=(x²-1)/(x²+1)²
y'=0
(x²-1)/(x²+1)²=0
(x-1)(x+1)/(x²+1)²=0
(x-1)(x+1)=0
x₁=-1 ; x₂=1
х (-1)(1)
y' + - +
y возрастает убывает возрастает
в точке х=1 минимум