Про квадратный трехчлен g(x) известно, что g(3)+g(5)=0 и g(2)+g(11)=0.найдите произведение корней уравнения g(x)=0

Пусть квадратный трехчлен имеет вид .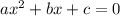

Умножим первое уравнение на (-13/8) и прибавим второе уравнение, получим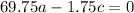 откуда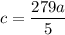

По теореме Виета

ответ: 55,8.

g(x) =ах²+вх+с

g(3)=а*3²+в*3+с; g(5)=а*5²+в*5+с

g(3)+g(5)=а*3²+в*3+с+а*5²+в*5+с=а*(9+25)+в*(3+5)+(с+с)=34а+8в+2с

g(3)+g(5)=0, значит, 34а+8в+2с=0; или 17а+4в+с=0

g(2)=а*2²+в*2+с; g(11)=а*11²+в*11+с

g(2)+g(11)=а*2²+в*2+с+а*11²+в*11+с=а*(4+121)+в*(2+11)+(с+с)=125а+13в+2с

g(2)+g(11)=0,значит, 125а+13в+2с=0;

Имеем систему двух уравнений с тремя  переменными

17а+4в+с=0;

125а+13в+2с=0;  Нас интересует с/а, поскольку по теореме Виета это и есть произведение корней квадратного уравнения.

Выразим из этих уравнений отношение с/а, из первого уравнения

с/а=-17-4в/а

Из второго уравнения с/а=-62.5-6.5в/а; приравняем эти выражения, найдем отношение в/а, получим

-17-4в/а=-62.5-6.5в/а; откуда

-17+62.5=(4-6.5)в/а, в/а=45.5/(-2.5)=-455/25=-18.2, зная это отношение, найдем

искомое с/а=-17-4в/а;  с/а=-17-4*1(-8.2)=-17+72.8=55.8