Про числа a и b известно что a + 1 / b равно 7 и b + 1 / a равно 8 найдите значение выражения ab + 1 / a b
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему повторяются слова не ожидали,неожиданность,неожиданное?...
2 - Переведи десятичную дробь в смешаную 2,4помагите...
3 - Определи, какой объём воды вытесняет корабль, если на него действует выталкивающая...
3 - Однородные члены — слова, которые перечисляются....
1 - Замени 2 неравенство двумя неравенствами 1) 10 x 302) 20 x 48...
3 - нужен развёрнутый ответ с примерами...
2 - Маша, Катя, Борис, Василиса бросают жребий кто будет начинать игру. Какова вероятность...
3 - Назовите по систематической номенклатуре следующие соединения...
3 - Обособленные уточняющие члены Укажите предложение, в котором есть обособленный...
1 - Запишите частное в виде дроби (у-1):(у^2+2)...
2
Составим систему и определим значения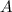 и
и 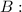
Высчитываем выражение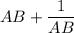 , подставляя значения букв
, подставляя значения букв 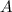 и
и 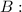
ответ: 54.