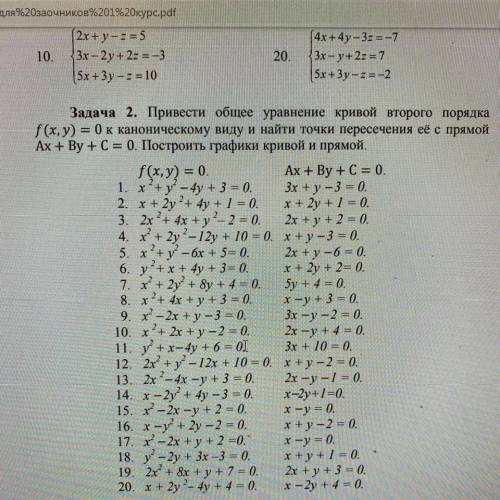
Привести общее уравнение кривой второго порядка к каноническому виду и найти точки пересечения ее с прямой x+2y^2-4y+4=0; x-2y+4=0 20 вариант
Другие вопросы по теме Алгебра
Популярные вопросы
- 127 бет,5-тапсырма. Мәтінді түсініп оқыңдар. Әр азат жолында не жайында айтылғанын...
2 - За 3 с маятник совершил 15 колебаний. Чему равны период и частота его колебаний?...
2 - ЗАПИТАННЯ І ЗАВДАННЯ? 1.Яке значення має транспорт для економіки?2.Якими...
1 - 4. При русі автобуса з прискоренням 1,25 м/с2 його швидкість зросла від 36...
3 - Объясните выражение Движение-это жизнь как эта фраза связана с данной Темой...
1 - Теңдеуді шешу;5x+7(3-x)=3(5-2x)-6...
3 - - тар, - тер — после глух. и звон. б, в, год Берілген сөздерді жікте (просклоняйте...
1 - Сочинение: «Нравственный выбор моего ровестника в произведениях В. П. Астафьева...
2 - СОР ПО ГЕОМЕТРИИ 7 КЛАСС (БЕЗ СПАМА...
2 - Как распознать газообразный продукт реакции(водовород)?...
3
Даны кривая x+2y²-4y+4=0 и прямая x-2y+4=0.
В уравнении кривой выделяем полный квадрат.
(2y²- 4y + 2) - 2 + х + 4 = 0,
2(у - 1)² = -х - 2,
(у - 1)² = (-1/2)(х + 2),
(у - 1)² = 2*(-1/4)*(х - (-2)), это каноническое уравнение параболы, ветви её направлены влево.
Вершина в точке (-2; 1).
Фокус в точке (-17/8; 1).